Les bons tuyaux d’Huggy : comment aller plus vite en descente
Comment aller plus vite en descente ? Une bonne question à laquelle se colle aujourd’hui notre ami Huggy.

Tout d’abord une petite précision : Huggy a simplifié au maximum les explications physiques et les intermèdes mathématiques, il utilise des termes parfois impropres ou peu précis et néglige certains phénomènes sans forcément l’expliciter clairement. Sachez bien qu’il est en conscient mais il a essayé de faire simple pour être compris du plus grand nombre.
Table des matières de la page
[2012/10/03 : update] :
-refonte de l’article et correction d’une erreur de calcul de l’article original (cf le forum)
[updates à venir] :
-graphique des distances parcourues en fonction du temps (et de l’aérodynamisme et de la masse)
-comparaison avec des situations réelles (freeride de St Mury, descente de Chessy en région parisienne)
[updates à venir encore plus tard si on a le temps] :
-évaluation de l’aérodynamisme avec et sans lycra
-influence de l’aspiration et vitesse max en ‘bob’
Comment aller plus vite
Le descendeur, en roller comme en ski, prend de la vitesse à cause de la pente et est freiné par la résistance de l’air.
Nous avons donc :
- ce qui fait accélérer : la pente. Plus c’est pentu, plus on va vite.
- ce qui fait freiner : la résistance de l’air. Cette résistance dépend de l’aérodynamisme du descendeur mais aussi de son poids (les frottements mécaniques, roulements et roues, sont négligeables) [14]
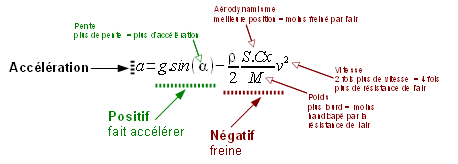
Quelques formules magiques et un peu trifouillage mathématique permettent de calculer la vitesse maximum que l’on peut attendre en descente.
Cette vitesse maximum dépend :
- du pourcentage de la pente : une pente quatre fois plus forte permettra d’aller deux fois plus vite,
- de l’aérodynamisme du descendeur,
- du poids du descendeur : un descendeur quatre fois plus lourd pourra aller deux fois plus vite.
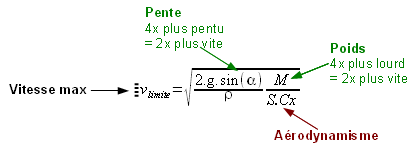
Plusieurs solutions donc pour aller plus vite :
- trouver une pente à 25%,
- améliorer sa position de recherche de vitesse,
- faire une cure de Big Mac.
La position de recherche de vitesse
Des études en soufflerie permettent de déterminer la position de recherche de vitesse optimale, permettant d’atteindre la vitesse la plus élevée ([ref 1]).
La meilleure posture correspond à une position où le dos est horizontal et arrondi, les épaules bombées, les bras dans le prolongement des jambes. L’important est qu’ils ne bouchent pas le pont entre les jambes.
Une position de recherche de vitesse plus assise sur les talons permet un meilleur aérodynamisme mais elle est physiquement beaucoup plus difficile à tenir.
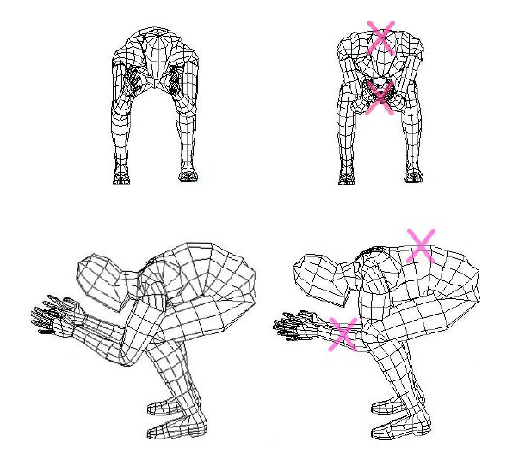
La position de recherche de vitesse optimale
La vitesse maximale
Pour un même descendeur les faibles variations de position peuvent entraîner une diminution de l’aérodynamisme de 10 à 20%, faisant chuter la vitesse maximum de 5 % à 10%.
Ci-dessous l’influence de la position sur la vitesse maximale (sur une pente à 10%)[6] :




Sur une pente à 12%, en adoptant une très bonne position (celle de la photo 1), un descendeur du gabarit de celui de la photo 1 pourrait atteindre une vitesse 119km/h.
119km/h : c’est extrêmement rapide. Quelques modifications simples permettent d’arriver à un résultat plus réaliste :
- aérodynamisme non optimal (à plus de 100km/h il devient difficile de garder une position de recherche de vitesse parfaite)
- pente de 10% ( à titre de comparaison, l’Alpe d’Huez c’est en moyenne 8% sur 14km, avec des passages un peu plus de 10%)
Vitesse maximale théorique: 102,5km/h, très proche de la vitesse réellement atteinte par un patineur bien connu dans cette descente.
L`influence du poids[8]
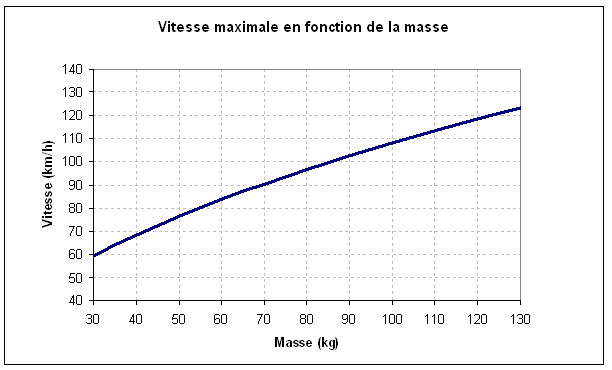
Tous les descendeurs en ont fait l’expérience : plus on est lourd et plus on va vite… Avec la même position aérodynamique (non optimale) sur une pente à 10%, un descendeur de 90kg pourra atteindre une vitesse de 103km/h alors qu’un descendeur de 60kg plafonnera à 84km/h.
Cette influence du poids du descendeur est confirmée lors des tests en soufflerie. Sur la photo ci-dessous, alors que les deux skieurs ont une position de recherche de vitesse optimale, dans une pente à 10% celui gauche (pesant 90kg) pourra atteindre une vitesse de 109km/h alors que celui de droite (pesant 60kg) ne dépassera pas les 100km/h.

Vitesse max : 109km/h pour le skieur de 90kg, 99km/h pour le skieur de 60kg
Atteindre sa vitesse maximale
Dans une pente à 10%, avec une très bonne position aérodynamique, la vitesse maximum d’un descendeur de 60kg est donc d’à peine moins de 100km/h. Or approcher les 100km/h en descente c’est extrêmement rare.
Là encore il y a une explication : la vitesse maximum calculée dans les paragraphes précédents est une vitesse limite qui n’est pas atteinte instantanément. Il faut un certain temps avant d’atteindre cette vitesse de pointe. Pire encore : si la prise de vitesse est assez rapide dans les premières secondes on accélère ensuite de moins en moins et plus on se rapproche de cette vitesse maximum plus la vitesse est dure à gagner.
Si notre descendeur de 60kg se lance à l’arrêt dans une pente à 10% avec une position assez moyenne :
- après 10 secondes il va être à 38% de sa vitesse maximum(soit 33km/h)
- après 20 secondes à 66% (58km/h)
- après 40 secondes à 92% (81km/h)
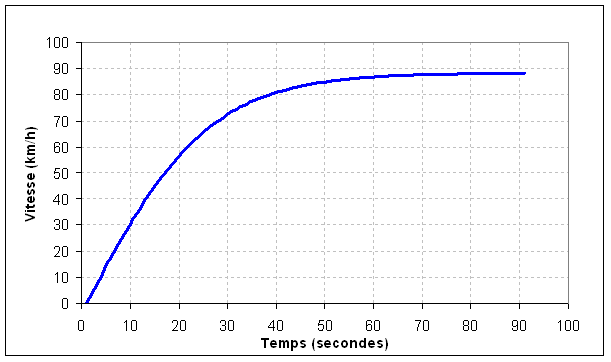
On s’aperçoit là que pour atteindre une vitesse élevée rapidement il est nécessaire de pousser assez fort lors des premiers mètres de la descente. En se laissant simplement descendre il faut un peu plus de 10 secondes pour atteindre 35km/h, vitesse qu’on peut atteindre bien plus rapidement en utilisant une poussée efficace. Au delà de cette vitesse il devient compliqué de continuer à pousser et il est plus optimal de rester en position de vitesse. En revanche, une fois atteinte la vitesse de 35 km/h, il faut encore près de 30 secondes pour atteindre 90% de la vitesse maximum.
En résumé, en se lançant à 35km/h du haut d’une descente à 10% il faut encore 30 secondes pour atteindre 90% de la vitesse maximale (soit 80km/h), Trente secondes de ligne droite dans une descente en 10% c’est long, c’est très long et ça explique qu’il soit difficile d’atteindre cette vitesse maximale.
Les limites de l`aérodynamisme
Comparons maintenant deux descendeurs du même poids, l’un dans une très bonne position de recherche de vitesse, l’autre en position de ‘freinage’ (relevé bras écartés), toujours sur une pente à 10%.
- vitesse limite du descendeur en position de vitesse : 109km/h
- vitesse limite du descendeur en position de freinage : 63km/h
Sans commentaires, tout le monde peut l’expérimenter : faire une descente sans se mettre en position aérodynamique fait perdre une vitesse considérable.
Dernier comparatif : un descendeur lourd, avec une très bonne position (90kg, rouge) et un descendeur léger, avec une position moyenne (60kg, bleu), tous les deux lancés dans une pente à 10%.
Le descendeur lourd a un gabarit est une position semblable à la photo ci-dessous. Sa vitesse maximum est de 109km/h.

Le descendeur léger a lui un gabarit est une position semblable à la photo ci-dessous. Sa vitesse maximum est de 88km/h.

Le schéma ci-dessous représente l’évolution de la vitesse des deux descendeur en fonction du temps.
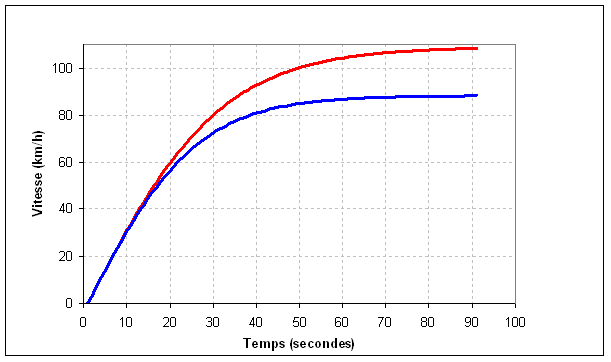
Le descendeur bleu, plus léger et avec une position moyenne, a une vitesse de pointe inférieure de plus de 20km/h au patineur rouge mais il faut attendre plus de 30 secondes pour qu’il y ait une différence de vitesse significative entre eux.
En pratique lorsqu’on se lance dans une descente on ne part jamais d’une vitesse nulle : on pousse un peu en haut de la pente pour accélérer un minimum avant de se mettre en position de vitesse. Dans l’hypothèse où les deux descendeurs se lancent dans la descente en ayant déjà une vitesse de 35 km/h le descendeur rouge sera à 74km/h 15 secondes après avoir arrêté de patiner alors que le bleu aura atteint une vitesse de 68km/h. La différence reste relativement faible.
Au final tout cela permet de s’apercevoir qu’il est important d’avoir une bonne position de vitesse lorsque l’on cherche à atteindre des vitesses très importantes mais qu’en compétition rechercher la position parfaite ne permet de gagner du temps que sur des descentes rapides et très longues. Sur un tracé sinueux le gain de temps se fera sur la trajectoire, les relances et les freinages et là au contraire les gros gabarits pourront être désavantagés.
Faut-il être lourd pour gagner ?
Si on prend cette étude au pied de la lettre on peut en conclure que plus on est lourd, mieux c’est. En effet, plus on est lourd, plus on va vite et en théorie la distance de freinage, et par la même occasion la vitesse de passage en virage, ne dépendent pas de la masse [ref 2]. Ce dernier point s’explique assez simplement par le fait qu’un lourd a certes plus d’énergie emmagasinée, mais il est aussi mieux “planté” dans le sol (il appuie plus fort donc il adhère mieux) ; donc au final un lourd est censé freiner aussi court qu’un léger.
Sauf que les constations sont unanimes : plus on est léger, plus on freine court et plus on passe les virages vite. Cette constatation est valable aussi bien dans le domaine de l’automobile [ref 3] que dans le domaine du roller.
Alors qu’en est-il? En fait, comme souvent la théorie néglige un peu trop de choses pour refléter parfaitement la réalité. La distance de freinage / passage en virage dépend indéniablement de la masse et le patineur lourd est toujours désavantagé par rapport au léger. Une explication se trouve dans le fait que lorsque les roues glissent (slide ou passage de virage), il y a des morceaux de gomme qui partent (les roues se cisaillent). Cette force de cisaillement est liée à la masse : plus le patineur est lourd, plus les roues vont se cisailler et plus la distance de freinage va augmenter. Une très bonne explication est donnée en annexe [ref 4]
Donc est ce qu’il faut être gros pour gagner ? La réponse est ça dépend !
- Si le tracé est long et quasiment tout droit (i.e. sans freinage), un patineur lourd (voire un vitesseux) a toutes les chances de gagner, pour peu qu’il développe une poussée en rapport avec sa masse (il faut les muscles en conséquences). Un tracé relativement droit comme la descente de Darnétal (freinages quasi inexistants et schuss est très long) va favoriser les descendeurs lourds.
- Si le tracé est très sinueux, les patineurs n’auront pas le temps d’atteindre des vitesses où la masse du patineur joue de manière significative (cf le paragraphe “Les limites de l’aérodynamisme”). Dans un tracé sinueux, le patineur léger a un avantage en sa faveur : il freine plus court et il peut passer plus vite dans les virages. Dans ce genre de tracés, les patineurs légers ont toutes leurs chances !
Précisions physiques et mathématiques
[1] On suppose que l’équation régissant le mouvement est 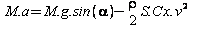 avec :
avec :
- M = masse du descendeur
- a = accélération du descendeur
- g = accélération de la pesanteur
- α = angle de la descente avec l’horizontale
- ρ = masse volumique de l’air
- S = maître couple du descendeur.
- Le maître couple est la projection, suivant sa trajectoire et sur un perpendiculaire à cette trajectoire, de la surface du descendeur.
- Cx = coefficient de traînée
- v = vitesse du descendeur
Écrite sous la forme 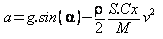 cette équation laisse clairement apparaître :
cette équation laisse clairement apparaître :
- un facteur « d’accélération » : g.sin(α), dépendant de façon directement proportionnelle[3] du pourcentage de la pente,
- un facteur « de freinage » :
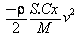 dépendant du carré de la vitesse[2], de l’ « aérodynamisme » S.Cx et de la masse M.
dépendant du carré de la vitesse[2], de l’ « aérodynamisme » S.Cx et de la masse M.
[2] En toute rigueur le coefficient de traînée Cx dépend du nombre de Reynolds et du nombre de Mach, eux-même fonctions de la vitesse.
[3] Le pourcentage de la pente n’est rien d’autre que la tangente de l’angle α que fait cette pente avec l’horizontale. Pour de faibles valeurs d’α, α = sin(α) = tan(α).
[4] L’équation [1] admet une solution analytique, la vitesse peut donc être explicitement exprimée en fonction du temps t : 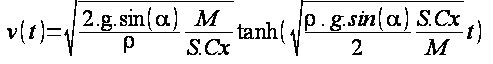
La limite lorsque t tend vers l’infini permet de déterminer la vitesse maximum pouvant être attente(ou plus exactement approchée) par le descendeur : 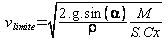
[5] Le terme « aérodynamisme du descendeur » désigne le facteur S.Cx, produit du maître couple et du coefficient de traînée.
[6] Les valeurs numériques utilisées sont :
- g = 9,81
- α = arctan(8/100)
- ρ = 1,204
- coefficient S.Cx/M de respectivement 0,00177 , 0,00220 , 0,00470 et 0,00530
[7] coefficient S.Cx/M égal à 0,002
[8] Influence de la masse du descendeur. Le terme poids est utilisé volontairement (bien que de façon impropre) en lieu et place du mot masse.
[9] Coefficient S.Cx/M égal à 0,002 pour le descendeur de 90kg, à 0,003 pour le descendeur de 60kg, La variation de maître couple n’est pas prise en compte.
[10] Coefficient S.Cx/M égal à 0,00177 pour le skieur de gauche, à 0,00215 pour le skieur de droite.
[11] Coefficient S.Cx/M égal à 0,00269
[12] Coefficient S.Cx/M égal à 0,00177 pour le descendeur en position de vitesse, à 0,0053 pour le descendeur en position de freinage.
[13] Coefficient S.Cx/M égal à 0,00177 pour le descendeur rouge, à 0,00269 pour le descendeur bleu.
[14] D’autres forces freinent le patineur en descente : la résistance au roulement, due à l’écrasement des roues principalement (et non pas aux roulements comment on peut le lire parfois). Un patineur bien connu a d’ailleurs fait l’expérience de cette déformation des roues en faisant des catchs à très haute vitesse : si la vitesse est trop élevée, la gomme finit par chauffer et fondre !
Dans notre article, on néglige cette résistance au roulement, car elle est réellement négligeable ! Les roues de roller se déforment peu par rapport à des pneus (cf le très mauvais roulage des coyotes) et des études dans le domaine du cyclisme (donc avec des pneus) ont montré que la résistance de l’air devient très rapidement et très largement prépondérante par rapport à la résistance au roulement (typiquement au dessus de 10-15 km/h).
[ref 1] Images et mesures issues du document de la FFS
« Ski alpin : effets aérodynamiques de la posture sur la performance » disponible sur : http://www.ffs.fr/pdf/dss/FFSdtninfo-biomeca-aeroposturealpin1.pdf
[ref 2] Masse et distance de freinage – la théorie
http://myelise.fr/entretien/boostage_files/masse%20et%20distance%20de%20freinage.pdf
[ref 3] “Le poids influence-t-il la distance de freinage d’un véhicule?” Mesures en conditions réelles
http://www.cstfelicien.qc.ca/Scinat/cyberexpojournal2005/w05m06.pdf
[ref 4] Le phéonène de cisaillement des roues, ou pourquoi la distance de freinage dépend de la masse
http://fgouget.free.fr/misc/freinage.shtml

Merci,
Tres tres bon article.
Il y a un travail très intéressant de Boris D. (ex du team Rossignol de descente) sur le sujet. De cette même époque, avec des gabarits si différents, comment Luc Lenoir mettait souvent Oscar Galiazzo dans le vent… si j’ose dire.
Great article, thanks for sharing, I have learned a lot!